《导数公式推导过程（导数运算法则的推导过程）》正文开始，本次阅读大概2分钟。

导数是函数值相对于自变量的瞬时变化率，求导数是一个取极限的过程。对于一个连续且可导的函数，其导数的定义如下

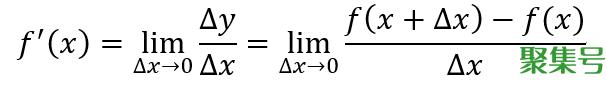
函数可导的前提是函数必须连续，对于连续函数，有下列等式成立

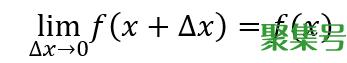
上式是函数在x处连续的定义。结合连续函数的定义和极限的运算性质，我们接下来推导导数运算法则。

两个函数相加的导数

假设F(x)为两个可导函数的和

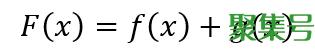
那么根据导数定义，F(x)的导数为

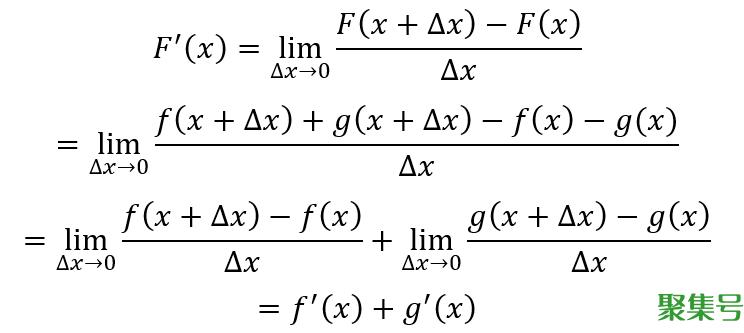
即两个可导函数的和的导数等于导数的和，导数运算减法同理。

两个函数乘积的导数

假设G(x)为两个可导函数的和

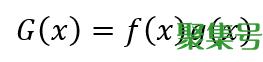
根据导数定义，G(x)的导数为

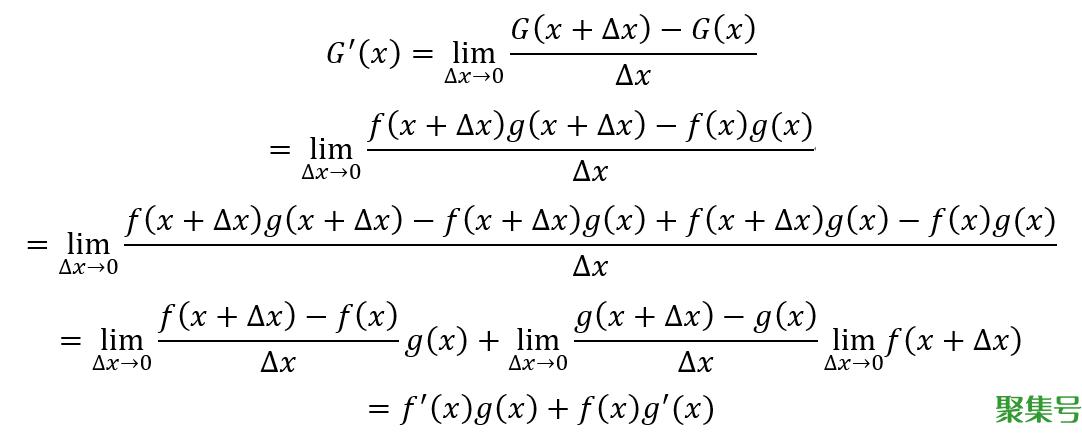
两个可导函数的乘积的导数的结果为

两个函数的比值的导数

假设H(x)为两个可导函数的比值

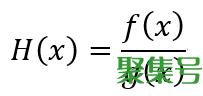
根据导数定义，那么H(x)的导数为

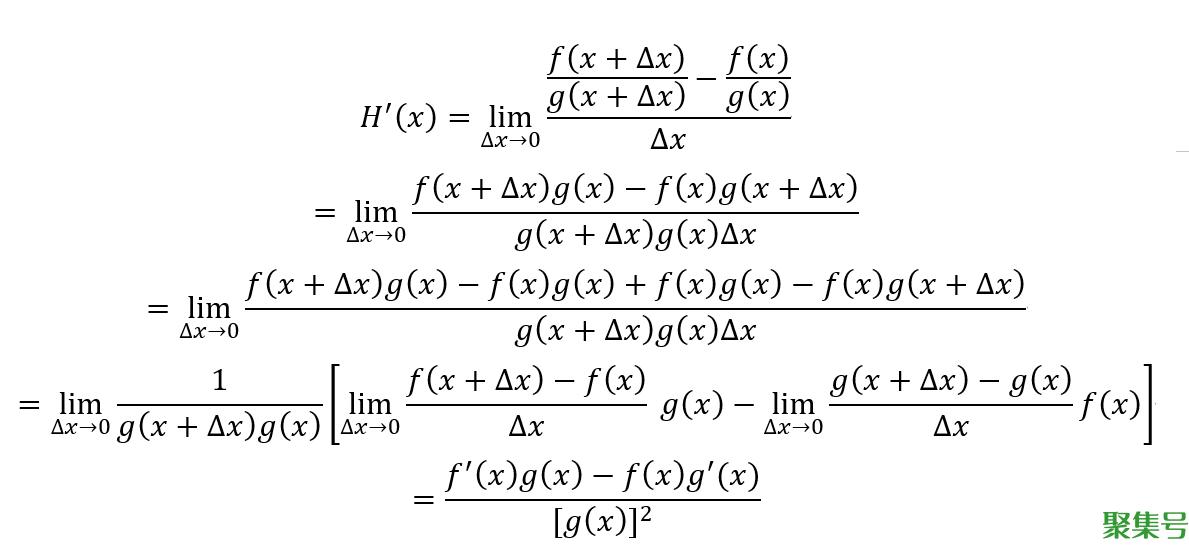
两个可导函数的比值的导数结果为

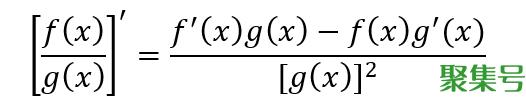
掌握推导过程可以帮助理解导数的定义和运算。