《世界上更大的数是什么最小的呢(世界上最小的数是几)》正文开始，本次阅读大概3分钟。

在数学上，数的个数是无限的，而且大小也是无限的。无论多大的数，都能找出比它更大的数。假设M是一个极大的数，哪怕给这个数加上0.0001，所得到的M+0.0001也会比M大。同样地，无论多小的数，也能找出比它更小的数，只要在它基础上再减去一个大于0的数即可。

因此，数学上并不存在更大的数，也不存在最小的数。不过，数学家倒是发现过一些非常大且有意义的数，它们能够大到难以想象的程度。另一方面，给非常大的数添上负号，就能得到非常小的数，所以要找最小的数等同于找更大的数。那么，数学家发现的更大有意义的数是多少呢？

更大的数

构造一个大数，很多人可能会首先想到指数或者阶乘。9^128相当于1.39×10^122，128!相当于3.85×10^215，这两个数已经远远超过了可观测宇宙中的粒子总数（10^80）。但在数学上，还有构造出更大数的 *** ，比如高德纳箭号表示法：

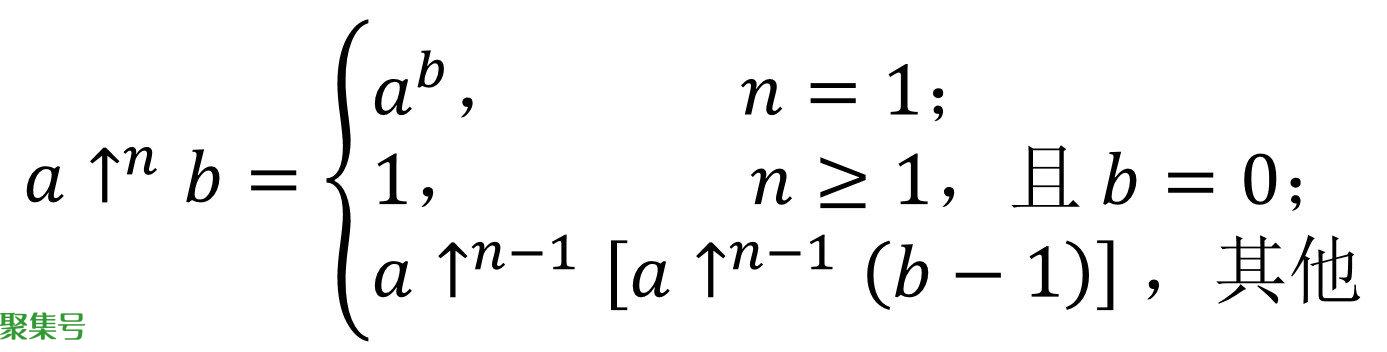
根据上式，如果a=3，和b=5，当n=1时，可得：

3↑5=3^5=3×3×3×3×3=243

当n=2时，3↑↑5这个数的大小会急剧增大：

3↑↑5=3^3^3^3^3=3^3^3^27=3^3^7625597484987≈3^(1.258×10^3638334640024)

3↑↑5这个数已经大到不可思议的程度，如果再加一层，3↑↑↑5更是大到无法想象的程度。

数学家葛立恒在解决与拉姆齐二染色定理有关的问题时，发现了一个当时被认为更大的数，后来被称为葛立恒数。这个数实在太大了，它的表示 *** 很特别，如下所示：

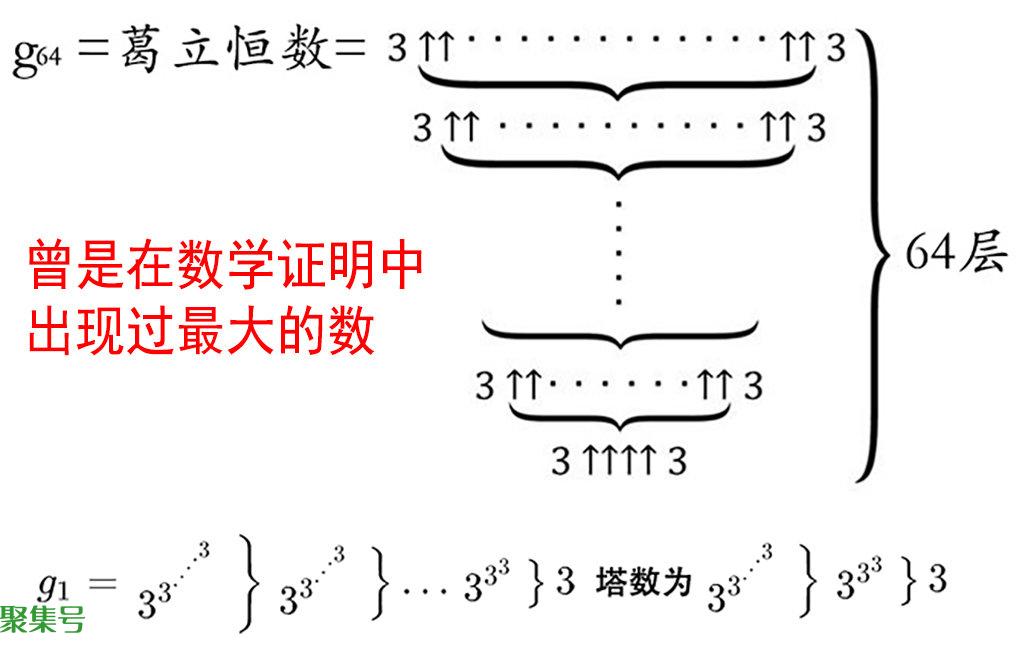
从下往上看，每一层的数都表示上一层的箭头个数。之一层为：

g(1)=3↑↑↑↑3=3↑↑↑[3↑↑↑(3↑↑↑3)]

3↑↑↑3=3^3^3……^3，这个指数塔中，共有7625597484987或者3^3^3个3

就g(1)而言，这个数已经大到无法用常规的方式表达。到了第二层，箭头个数变成了g(1)个，这一层的数会更加大幅增长。而葛立恒数总计64层，每增加一层，数就会急剧增大。葛立恒数之大超乎想象，如果要把这个数完全展开，在直径930亿光年的可观测宇宙中，每个最小的普朗克空间（4×10^-105立方米）写一个数，也远远写不完葛立恒数的所有数。

后来，数学家又发现了超越葛立恒数的数，当然不是“葛立恒数+1”，或者“葛立恒数^葛立恒数”，因为这些数没有什么意义。这个更大的数与矩阵树定理中的TREE函数有关，这是一个增长速度极快的函数。

TREE函数增长快到什么程度呢？TREE(1)=1，TREE(2)=3，乍一看这个函数不咋样。然而，到了TREE(3)，这个数突然暴增到不可思议的巨大程度。TREE(3)比葛立恒数，就像葛立恒数比1。

TREE(3)的更大纪录也被打破了，因为还有比TREE函数增长速度快得多的SSCG函数。SSCG(0)=2，SSCG(1)=5，这个函数一开始也是增长很慢，但SSCG(2)已经达到了3×2^(3×2^95)-8，相当于3后面跟了3万亿亿亿个0。到了SSCG(3)，这个数已经远远超过TREE(TREE(...TREE(3)...))，总嵌套层数为TREE(3)个，葛立恒数在它面前小到近乎为0。SCG是与SSCG相近的函数，其增长速度还要更快，SCG(3)还要大于SSCG(3)。

最小的数

如果要说数学中最小的数，可以在给SCG(3)加个负号，-SCG(3)可以小到不可思议的程度。如果要说科学意义上最小的数，各种普朗克单位就非常小，比如上面提到的1普朗克空间，数量级在10^-105。更小可以小到0，那就是0开氏度的绝对零度，但这个温度在现实中无法达到。