《圆周率是谁发明的(圆周率是谁发明的人叫什么名字)》正文开始,本次阅读大概3分钟。
祖冲之是我国古代著名的数学家和天文学家,他在数学上最重要的成就是把圆周率的小数位史无前例地计算到第七位,这个精度在随后的800年里一直是世界之一。那时是公元480年,一切都要依靠手工计算的时代(甚至算盘可能还没有出现),算个开方都费劲,那么,祖冲之是如何算出精度这么高的圆周率呢?
圆周率并不是通过先作圆,然后量周长和直径,最后算出来的。因为这样做的误差很大,测量误差不可避免。事实上,古代数学家在很长一段时间里都是用几何 *** 来计算圆周率。
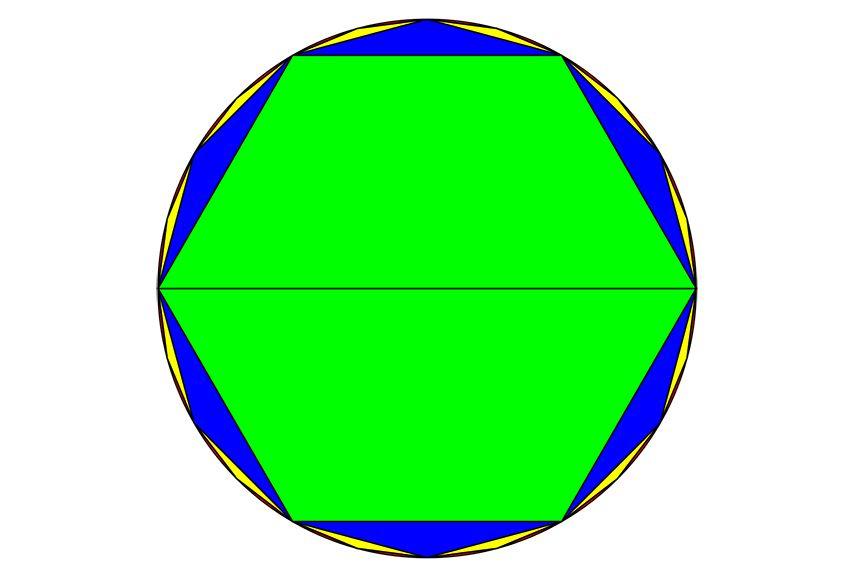
祖冲之算圆周率所使用的 *** 是刘徽发明的割圆术,这与阿基米德所用的 *** 有些不同。阿基米德通过做圆的外切和内接正多边形,来计算圆周率的上下限,因为边数越多的正多边形越接近于圆。
刘徽的割圆术基于圆的内接正多边形,他用正多边形的面积来逼近圆的面积。分割越多,内接正多边形和圆之间的面积越来越小,两者越来接近。无限分割之后,内接正多边形和圆将会合二为一。
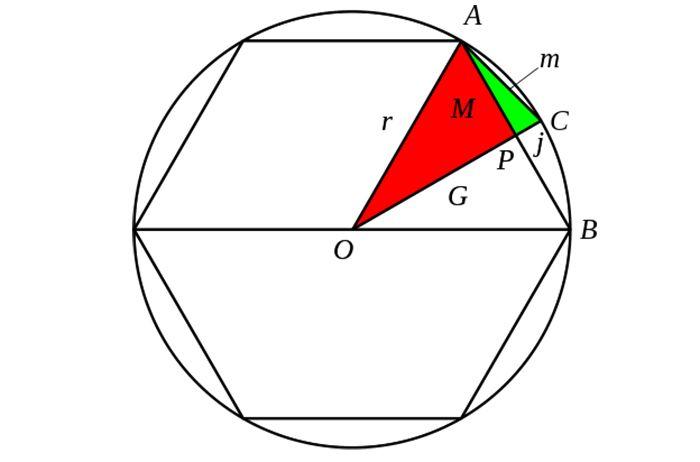
如上图所示,在一个半径为r的圆中做正3×2^n(n为正整数)边形,假设其边长为a_n,即AB=a_n。AB的中点为P,连接OP交圆于C。那么,AC和BC就是正3×2^(n+1)边形的边长,可以表示为a_(n+1)。
在直角三角形AOP中,根据勾股定理:
OA^2=AP^2+OP^2
令OP=b_n,由此可得:
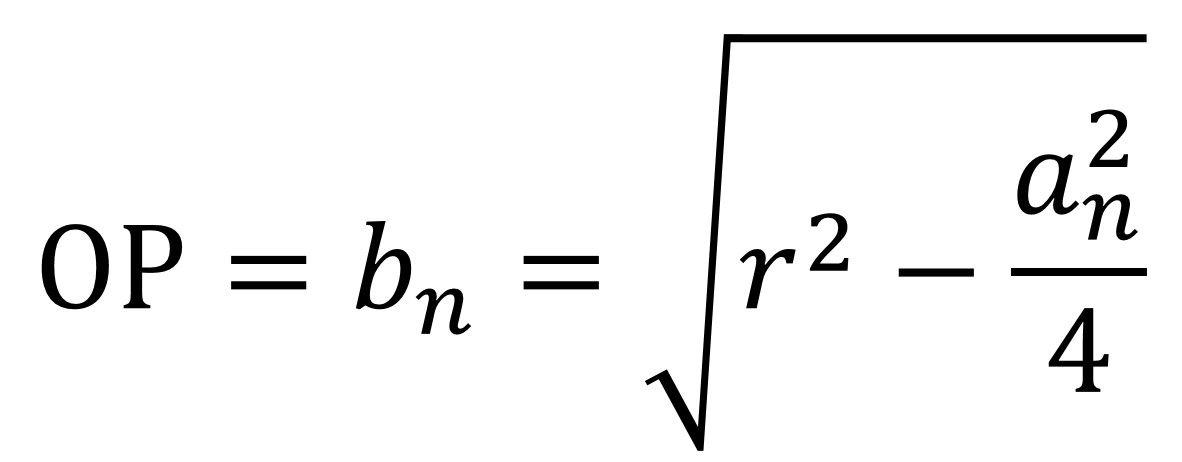
令PC=c_n,c_n=PC=OC-OP=r-b_n
在直角三角形APC中,根据勾股定理:
AC^2=AP^2+PC^2
由此可得:
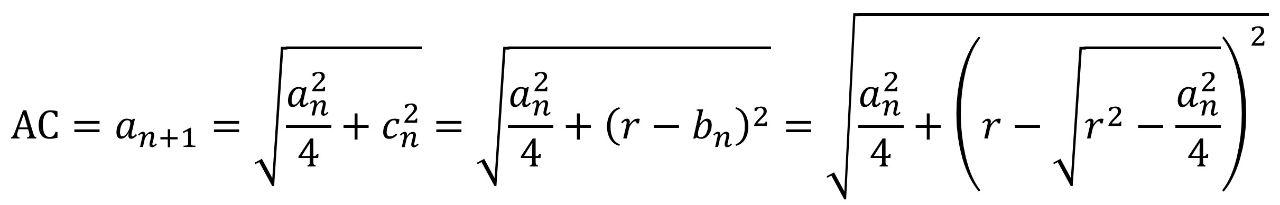
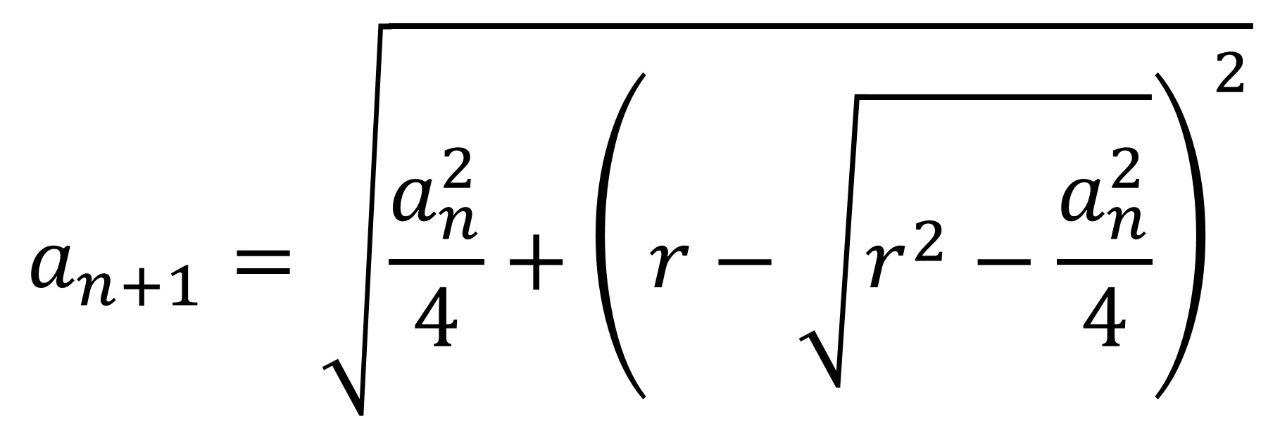
知道正3×2^n边形的边长之后,再根据刘徽多边形面积公式,可以算出正6×2^n边形的面积。根据上述正多边形边长的迭代公式,不断的把圆分割下去,圆面积的计算精度会越来越高。
在刘徽的 *** 中,引入了极限和无穷小分割的思想。刘徽的 *** 更为巧妙,也更为简洁。刘徽算到了正3072边形,结果得到的圆周率为3.1416。

祖冲之在刘徽割圆术的基础上,算到了正24576边形,并根据刘徽圆周率不等式,确定了圆周率的下限(肭数)为3.1415926,上限(盈数)为3.1415927。并且,祖冲之还顺便给出了圆周率的一个近似分数355/113,其前六位都是正确的。
在没有计算机和算盘的帮助下,祖冲之用算筹来计算乘方和开方,硬生生地把圆周率的小数位算到了第七位,这需要极其巨大的毅力和艰苦卓绝的付出。在祖冲之的努力下,此后800年里,没有人能够算出比这精度更高的圆周率。
 Villain博客
Villain博客